Numerical Methods in Accelerator Physics

Lecture Series by Dr. Adrian Oeftiger

Lecture 1

Run this notebook online!

Interact and run this jupyter notebook online:

via the public mybinder.org service:
mybinder.org logo
via the public gesis.org service:
gesis.org logo (enter as github repository name: aoeftiger/TUDa-NMAP-2023 and ref: v1.0 )

Also find this lecture rendered as HTML slides on github $\nearrow$ along with the source repository $\nearrow$.

Run this first!

Imports and modules:

In [1]:
from config import *
%matplotlib inline

Today!

  1. About Accelerators
  2. Time Scales
  3. Modelling a Pendulum ($\leadsto$ rf cavities focusing a beam)

Accelerator Physics

Accelerator physics $\Longleftrightarrow$ plasma physics

  • single-particle effects: non-linear dynamics
  • multi-particle effects: collective instabilities

What is an "accelerator"?

$$\begin{array}\,\text{beam self fields} &>& \text{external applied fields} &\text{(plasma)} \\ \text{beam self fields} &\ll& \text{external applied fields}& \text{(accelerator)}\end{array}$$

$\implies$ perturbation technique applicable to higher-energy accelerators:

$$\begin{cases} \text{unperturbed motion} &=& \text{external fields} \\ \text{perturbation} &=& \text{self fields} \end{cases}$$

Large part of this course: model effects on particle beam due to external fields!

Accelerator Fundamentals

Putting it simple: 3 major ingredients

  • radio frequency (rf) cavities for bunching and acceleration
  • dipole magnets for steering
  • quadrupole magnets for (transverse) focusing

$\implies$ enforce oscillations to contain particles!

One "Electron Volt"

1 eV $=$ gained kinetic energy of particle with elementary charge after traversing 1 V potential difference

Common Higher-energy Accelerator Types

Linacs

  • steady, intense beams
  • protons/ions and electrons
UNILAC at GSI image: UNILAC at GSI, Darmstadt

Cyclotrons

  • low energy (limited by relativistic effects)
  • protons/ions
  • provide muons, neutrons, isotopes
  • medical applications and research
Cyclotron at PSI image: PSI cyclotron, Villigen (CH)

Synchrotrons

  • highest energies
  • slowly ramp up energy of beam
  • protons/ions: fundamental research
  • electrons: synchrotron light sources
LEIR at CERN image: LEIR at CERN, Geneva (CH)

FAIR complex at GSI

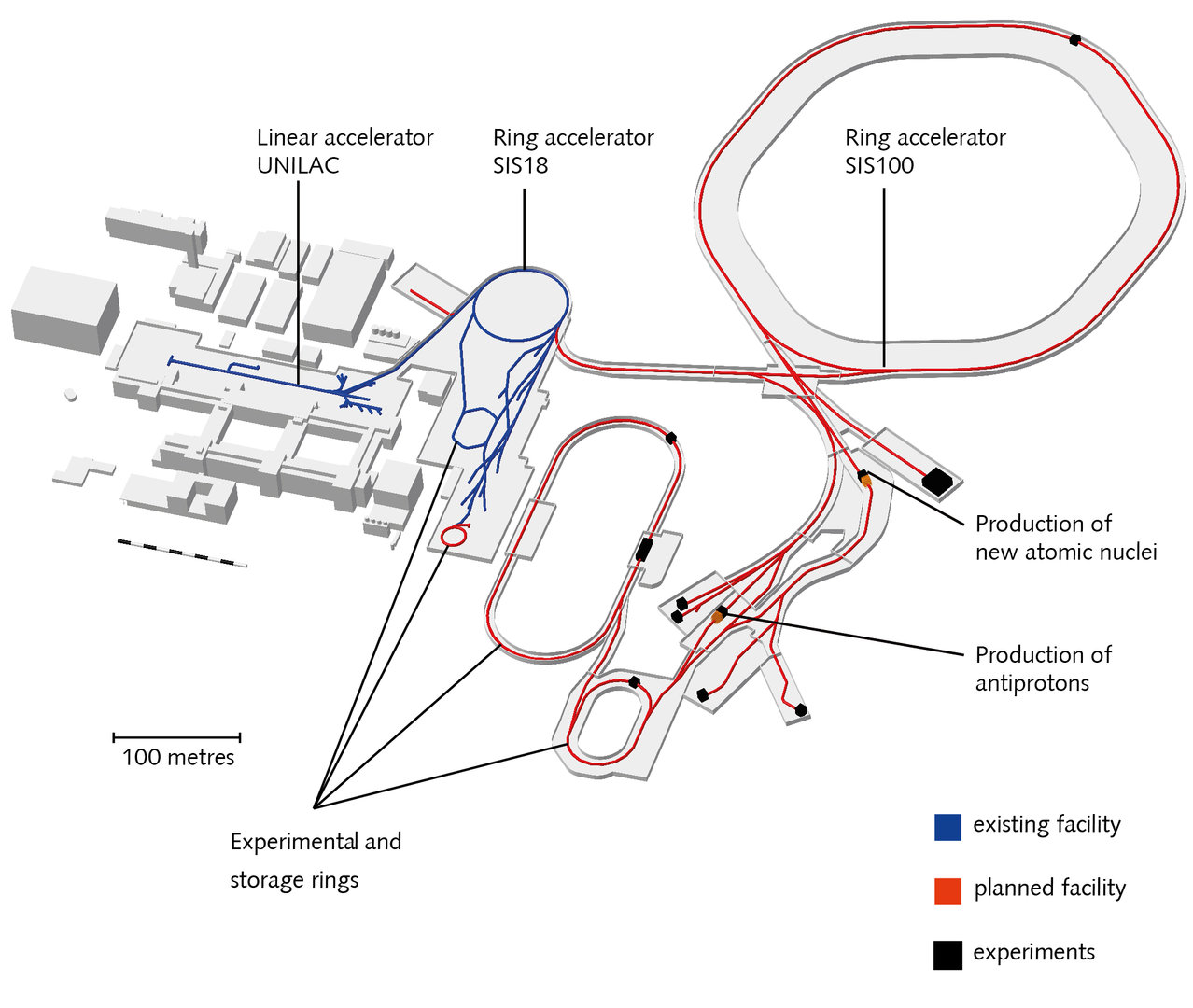
FAIR accelerator complex at GSI

Protons..Uranium for FAIR experiments:

  • UNILAC: $\sim$ 11 MeV/u
  • SIS18: $\leq$ 1 GeV/u (Uranium) or 4.5 GeV (protons)
  • SIS100: $\leq$ 10 GeV/u (Uranium) or 29 GeV (protons)

image: GSI - FAIR 2022

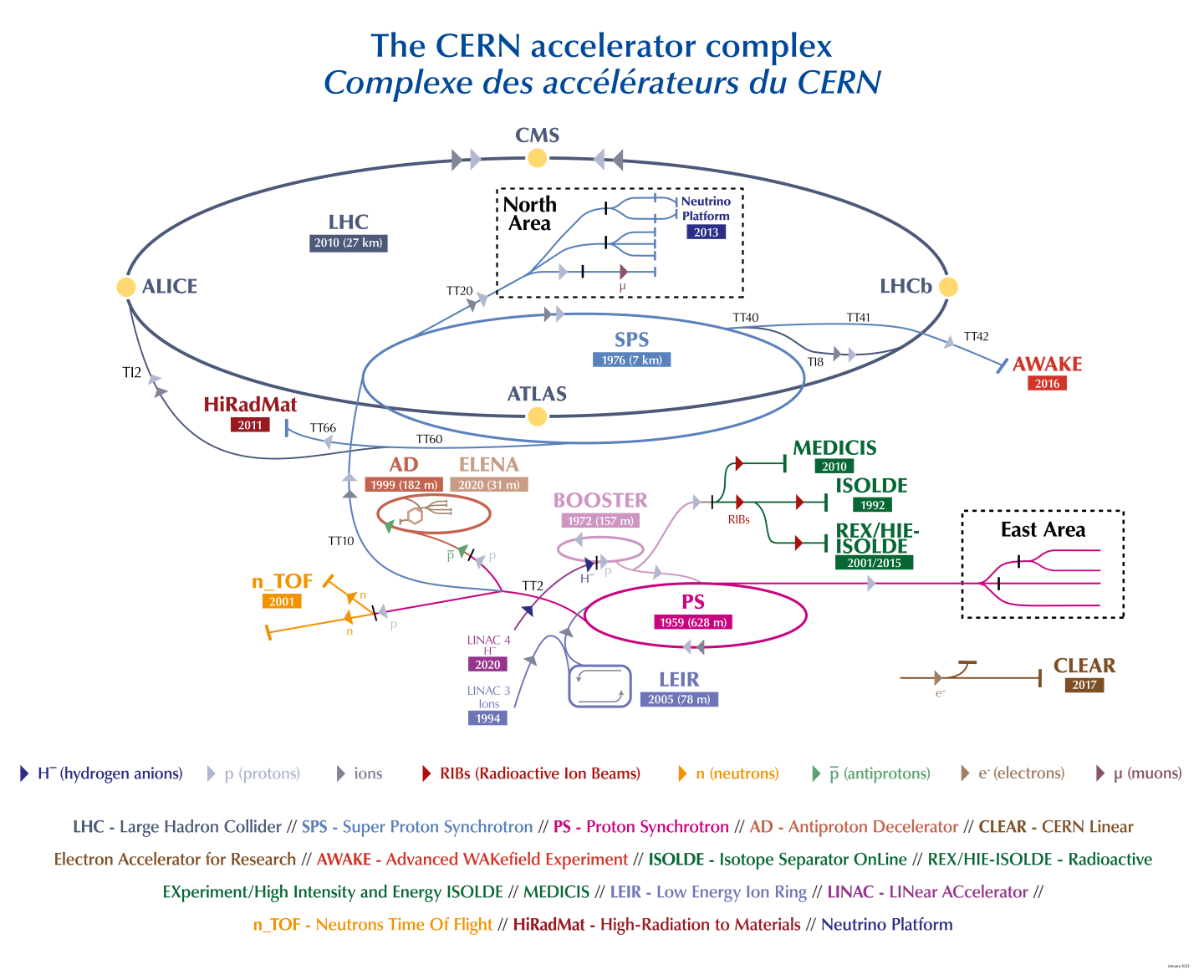
CERN accelerator complex

CERN complex

Protons for LHC injection:

  • LINAC4: 160 MeV
  • PSB: 2 GeV
  • PS: 26 GeV
  • SPS: 450 GeV
  • LHC: 7 TeV

image: CERN 2022

World-record LHC Fill Duration

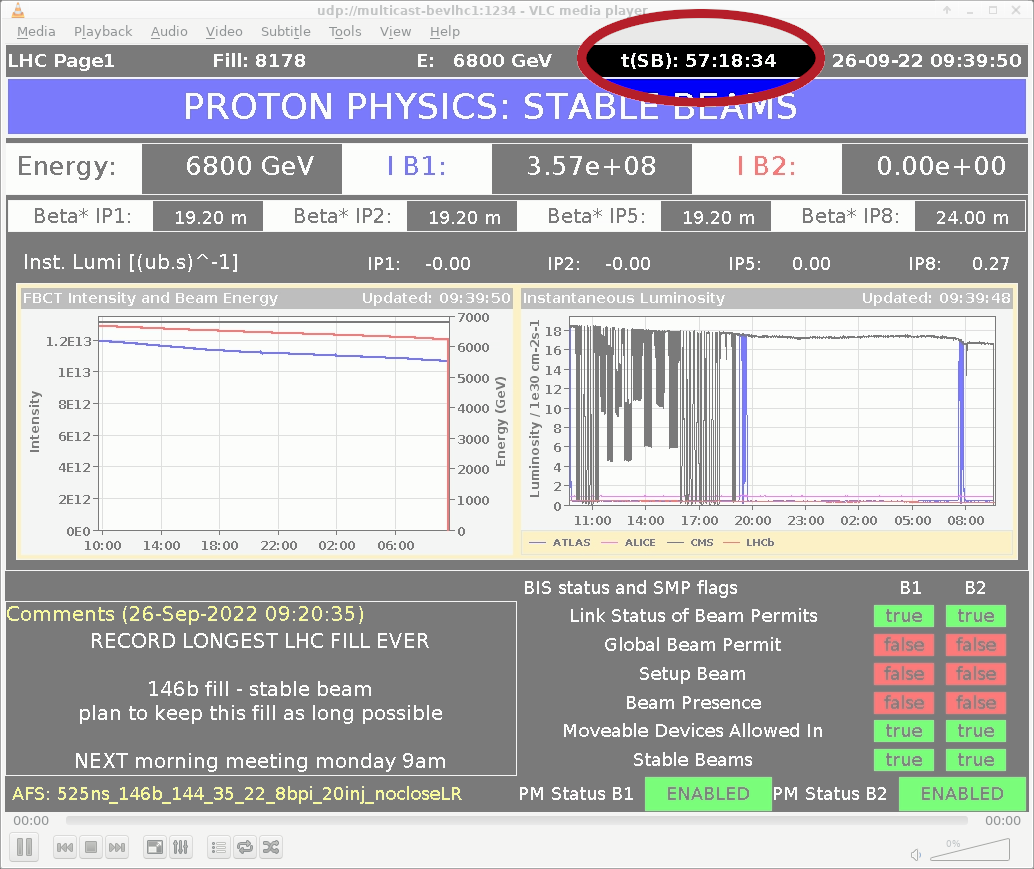
image: CERN LHC OP logbook 2022

$\leadsto$ 57h of beam storage $=$ how many turns in 27 km long LHC?

In [ ]:

Time Scales in a Synchrotron

A turn $\sim$ 1..100 μs:

  • many per turn: transverse (betatron) oscillations
  • once per turn: observation in a wall current monitor
  • 100s of turns: longitudinal (synchrotron) oscillations
  • 100s of turns: $e$-fold damping time of feedback systems
  • 100'000s to $>$ millions of turns: storage times

(compare: stability of the Earth's orbit around the Sun (age: 4.6 My))

Accuracy Required!

Analytical models do not suffice for quantitative understanding!

$\implies$ require detailed numerical models

$\implies$ predict and control stability over these time scales!

$\implies$ learn about basic concepts in this lecture! :-)

In the following...

Use simple pendulum to demonstrate development of numerical simulation model!

Clarify concepts:

  • phase space, Hamiltonian
  • discrete integration
  • symplecticity
  • 3 error sources of such simulation models:
    • discretisation
    • next time: numerical artefacts, modelling errors

The Nonlinear Pendulum

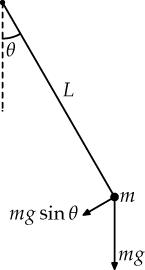
simple pendulum
  • point mass $m$ suspended on (weightless/inextensible) rod of length $L$
  • gravitational acceleration $g$ pulls $m$ downwards
  • degree of freedom: displacement angle $\theta$ of $m$ over time $t$
$$\begin{align} \text{Newtonian force}:& &m\frac{d^2\theta}{dt^2} &= -mg\frac{\sin\theta}{L} \end{align}$$

$\implies$ second-order non-linear ODE (ordinary differential equation)

$\leadsto$ numerical integration should give expected periodic movement!

image: simple.wikipedia.org

Phase Space

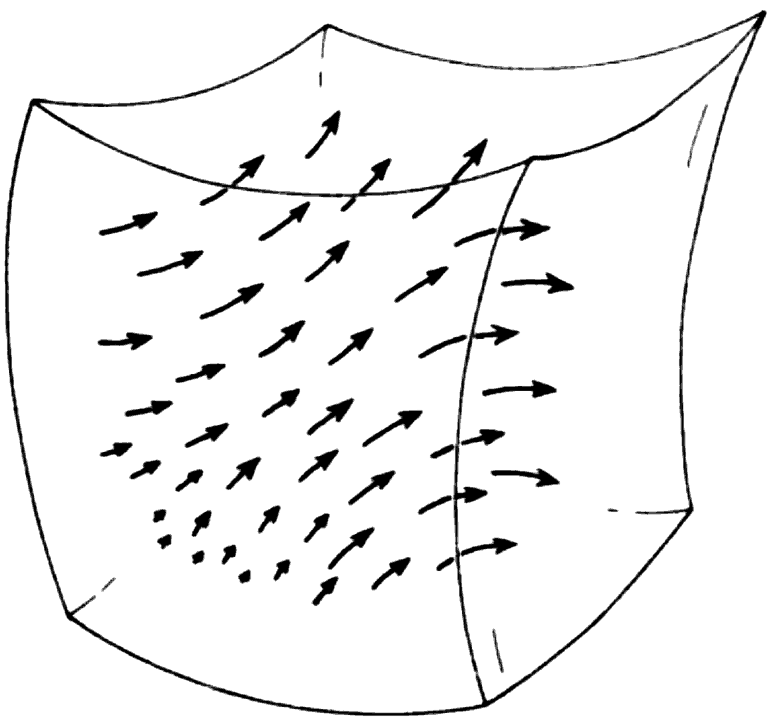
phase-space sketch

Very useful concept in classical mechanics:

  • collect all states of dynamical system
  • for $i$ degrees of freedom:
    each coordinate $q_i$ has associated conjugate momentum $p_i$
  • momentary state vector $(q_i, p_i)$ evolves with time $t$
  • equations of motion (e.o.m.) connect $(q_i, p_i)$ with each other:
    phase-space trajectories are solution of e.o.m.
  • rich structure, "symplectic manifold", phase space $=$ incompressible fluid:
    • phase-space trajectories are unique $\implies$ never overlap/cross
    • Liouville's theorem: local trajectory density does not change

image: Roger Penrose,
The Road of Reality

$\implies$ we will clarify via examples!

Conjugate Momentum

Consider $$p \doteq m L^2 \frac{d\theta}{dt}$$

(use Lagrangian functional to construct $p$ -- not focus of this lecture, see e.g. here for more details)

2nd-order ODE equation of motion $\leadsto$ 2 coupled 1st-order ODEs: evolution of $(\theta, p)$

$$\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin\theta = 0 \quad \Longleftrightarrow \quad \left\{\begin{array}\, \cfrac{d\theta}{dt} &= \cfrac{p}{mL^2} \\ \cfrac{dp}{dt} &= -m g L\sin\theta \end{array}\right.$$

Let's plot in phase space!

In [2]:
m = 1
g = 1
L = 1
In [3]:
def plot_arrow(theta, p, dt=1):
    # equations of motion:
    dtheta = p / (m * L*L) * dt
    dp = - m * g * L * np.sin(theta) * dt
    
    # plotting
    plt.scatter([theta], [p], s=50, c='r', marker='*', zorder=10)
    plt.annotate('', 
                 xytext=(theta, p), 
                 xy=(theta + dtheta, p + dp), 
                 arrowprops=dict(facecolor='black', shrink=0.03))
In [4]:
plot_arrow(1, 0)
# plot_arrow(0, -1)
# plot_arrow(-1, 0)
# plot_arrow(0, 1)
# plot_arrow(1/1.41, 1/1.41)

# # increase momentum:
# for i in np.arange(0.4, 2.5, 0.2):
#     plot_arrow(0, i)

# # increase angle:
# for i in np.arange(1, np.pi * 1.1, 0.2):
#     plot_arrow(i, 0)

set_axes()

Conservation of Energy

Equation of motion for $\theta(t)$: $$\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin\theta = 0$$

$$\begin{align} \text{Potential energy}:& &U &= mgL(1 - \cos\theta) \\ \text{Kinetic energy}:& &T &= \frac{1}{2}mL^2\left(\frac{d\theta}{dt}\right)^2 \end{align}$$
Conservation of total energy: $$T + U = \mathrm{const} \quad \Longleftrightarrow \quad \frac{d}{dt}(T + U) = 0$$

The Hamiltonian

$\mathcal{H} \doteq T + U$ is an example of a Hamiltonian functional on $\theta(t),p(t)$.

  • integral of motion (total energy) when $\mathcal{H}$ not explicitly depending on time
  • equations of motion $=$ gradient of Hamiltonian w.r.t. phase-space coordinates $(q_i,p_i)$
$$\begin{align}\, \frac{d}{dt}q_i & = \frac{\partial \mathcal{H}}{\partial p_i} \\ \frac{d}{dt}p_i &= -\frac{\partial \mathcal{H}}{\partial q_i} \end{align}$$
  • in 2D: contours of constant Hamiltonian value $=$ phase-space trajectories

Hamiltonian of the Pendulum

$$\mathcal{H} = T + U = \frac{1}{2} \frac{p^2}{mL^2} + m g L \left(1 - \cos\theta\right)$$

and correspondingly the 2 coupled 1D equations of motion via the Hamilton equations:

$$\left.\begin{array}\, \cfrac{d\theta}{dt} = \cfrac{\partial\mathcal{H}}{\partial p} \\ \cfrac{dp}{dt} = -\cfrac{\partial\mathcal{H}}{\partial\theta} \end{array}\right\} \quad \Longleftrightarrow \quad \left\{\begin{array}\, \cfrac{d\theta}{dt} &= \cfrac{p}{mL^2} \\ \cfrac{dp}{dt} &= -m g L\sin\theta \end{array}\right.$$
In [5]:
def hamiltonian(theta, p):
    T = p * p / (2 * m * L*L)
    U = m * g * L * (1 - np.cos(theta))
    return T + U
In [6]:
TH, PP = np.meshgrid(np.linspace(-np.pi * 1.1, np.pi * 1.1, 100), 
                     np.linspace(-3, 3, 100))

HH = hamiltonian(TH, PP)

plt.contour(TH, PP, HH, levels=10)
plt.colorbar(label=r'$\mathcal{H}(\theta, p)$')

set_axes()
In [7]:
TH, PP = np.meshgrid(np.linspace(-np.pi * 1.1, np.pi * 1.1, 100), 
                     np.linspace(-3, 3, 100))

HH = hamiltonian(TH, PP)

plt.contourf(TH, PP, HH, cmap=plt.get_cmap('hot_r'))
plt.colorbar(label=r'$\mathcal{H}(\theta, p)$')

plot_arrow(2, 0)

set_axes()

Observations: Pendulum Phase-space Topology

  1. origin $(0,0)$: stable fixed point
  2. bound motion (circular phase-space trajectories) close to origin
    ($\Leftrightarrow$ pendulum swinging back and forth)
  3. at larger angles towards $|\theta|\lesssim \pi$ change of angle slows down
  4. unstable fixed points at $|\theta|=\pi$
  5. unbound motion (continuous phase-space trajectories) at large momenta
    ($\Leftrightarrow$ pendulum moves in one angular direction only)
  6. separatrix: phase-space boundary separating bound from unbound motion

Summing up Concepts

  • phase space: all momentary states $(\theta, p)$ of the dynamical system
  • Hamiltonian $\mathcal{H}$: shapes landscape / geometry of phase space $\implies$ equations of motion
$\mathcal{H}$ contains the physics!

$\implies$ let's go ahead and apply discrete integrators to simulate the pendulum

$\leadsto$ Hamiltonian contours indicate exact geometry of solutions to the pendulum e.o.m. for comparison

Discretisation

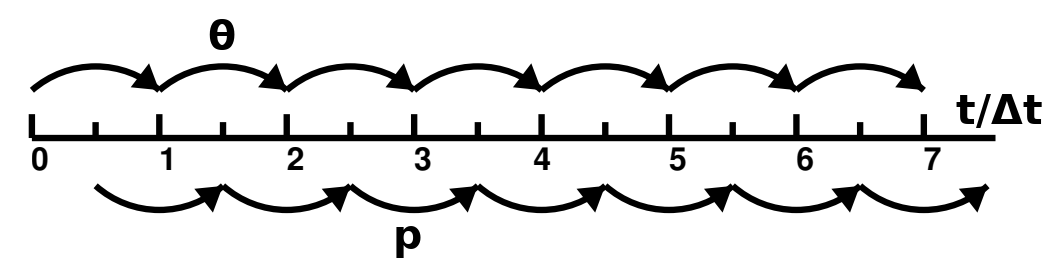
differential equation with continuous parameter $t$ $\stackrel{\text{discretise}}{\implies}$ discrete map with time steps $t=k\Delta t$

Start with Forward Integration

Assume constant values during $\Delta t$: "Explicit Euler method"

$$\left.\begin{array}\, \cfrac{d\theta}{dt} &= \cfrac{p}{mL^2} \\ \cfrac{dp}{dt} &= -m g L\sin\theta \end{array}\right\} \quad \stackrel{\text{Euler}}{\Longrightarrow} \quad \left\{\begin{array}\, \theta_{k+1} &= \theta_k + \Delta t\cdot\cfrac{p_{k}}{mL^2} \\ p_{k+1} &= p_k - \Delta t\cdot m g L\sin\theta_k \end{array}\right.$$
In [8]:
def solve_euler(theta, p, dt=0.1):
    theta_next = theta + dt * p / (m * L*L)
    p_next = p - dt * m * g * L * np.sin(theta)
    return (theta_next, p_next)
In [9]:
theta_ini = -1.1
p_ini = 0
n_steps = 100
In [10]:
results_euler = np.zeros((n_steps, 2), dtype=np.float32)
results_euler[0] = (theta_ini, p_ini)

for k in range(1, n_steps):
    results_euler[k] = solve_euler(*results_euler[k - 1])
In [11]:
plt.contour(TH, PP, HH, levels=10, linestyles='--', linewidths=1)

plt.plot(results_euler[:, 0], results_euler[:, 1], c='b')

set_axes()

$\implies$ Is there something qualitatively wrong with our integrator?

Total Energy should be conserved?

In [12]:
plt.plot(
    hamiltonian(results_euler[:, 0], results_euler[:, 1]), 
    c='b', label='Euler integrator')
plt.axhline(hamiltonian(theta_ini, p_ini), c='r', label='theory')

plt.xlabel('Steps $k$')
plt.ylabel(r'$\mathcal{H}(\theta, p)$')
plt.legend();

$\implies$ discrete pendulum model violates energy conservation

Even worse:

In [13]:
theta_ini2 = -3.
p_ini2 = 0
n_steps = 100
In [14]:
results_euler2 = np.zeros((n_steps, 2), dtype=np.float32)
results_euler2[0] = (theta_ini2, p_ini2)

for k in range(1, n_steps):
    results_euler2[k] = solve_euler(*results_euler2[k - 1])
In [15]:
plt.contour(TH, PP, HH, levels=10, linestyles='--', linewidths=1)
plt.plot(results_euler2[:, 0], results_euler2[:, 1], c='b')
set_axes()

Change from bound to unbound region?

Hamiltonian value of separatrix: $\mathcal{H}_{sep} = \mathcal{H}(-\pi, 0)\qquad$ (at unstable fixed point)

In [16]:
h_sep = hamiltonian(-np.pi, 0)
h_sep
Out[16]:
2.0
In [17]:
plt.plot(
    hamiltonian(results_euler2[:, 0], results_euler2[:, 1]), 
    c='b', label='Euler integrator')
plt.axhline(hamiltonian(theta_ini2, p_ini2), c='r', label='theory')
plt.axhline(h_sep, c='k', label='$\mathcal{H}_{sep}$')

plt.xlabel('Steps $k$')
plt.ylabel(r'$\mathcal{H}(\theta, p)$')
plt.legend(bbox_to_anchor=(1.05, 1))
plt.ylim(top=2.1);

Conclusion from Euler Integrator

  • violates energy conservation: increasing energy / amplitude continuously
  • even breaks underlying structure of original phase space: leaving bound motion region to unbound region
$\implies$ discretisation error!
(... think of implications for predicting LHC stability or Earth's orbit)

Symplecticity

Euler method is a non-symplectic integrator, i.e. breaks Hamiltonian nature and Liouville theorem.

Instead, numerical integrator mapping should preserve phase-space density (be symplectic)!

$\implies$ Jacobian $\mathbb{J}$ of map should satisfy $\det(\mathbb{J})\mathop{\stackrel{!}{=}} 1$

Euler method violates this, e.g. for pendulum:

$$\mathbb{J}_{Euler} = \begin{pmatrix} \cfrac{\partial\theta_{k+1}}{\partial\theta_k} & \cfrac{\partial\theta_{k+1}}{\partial p_k} \\ \cfrac{\partial p_{k+1}}{\partial\theta_k} & \cfrac{\partial p_{k+1}}{\partial p_k} \end{pmatrix} = \begin{pmatrix} 1 & \cfrac{\Delta t}{mL^2} \\ -\Delta t\, mgL\cos\theta_k & 1 \end{pmatrix} \implies \det\left(\mathbb{J}_{Euler}\right) \neq 1$$

Euler-Cromer Method

Let's fix symplecticity / phase-space volume preservation!

Euler has approximation error $\mathcal{O}(\Delta t^2)$.

$\implies$ add cancellation term of same magnitude (simplify $m=L=g=1$):

$$\mathbb{J}_{EC} = \begin{pmatrix} 1 & \Delta t \\ -\Delta t\cos\theta_k & 1 \color{red}{-\Delta t^2\cos\theta_k} \end{pmatrix} $$
$$\implies \det\left(\mathbb{J}_{EC}\right) = 1$$

Euler-Cromer Method II

Main difference to Euler method: "staircase" movement in phase space

  • first update $\theta$
  • then update $p$
$$\left.\begin{array}\, \cfrac{d\theta}{dt} &= \cfrac{p}{mL^2} \\ \cfrac{dp}{dt} &= -m g L\sin\theta \end{array}\right\} \quad \stackrel{\text{Euler-Cromer}}{\Longrightarrow} \quad \left\{\begin{array}\, \theta_{k+1} &= \theta_k + \Delta t\cdot\cfrac{p_{k}}{mL^2} \\ p_{k+1} &= p_k - \Delta t\cdot m g L\sin\color{red}{\theta_{k+1}} \end{array}\right.$$

Euler-Cromer Method III

Illustration of stair-case movement in phase space for linear pendulum where $\sin\theta\approx \theta$:

$$\left\{\begin{array}\, \theta_{k+1} &= \theta_k + \Delta t\cdot p_{k} \\ p_{k+1} &= p_k - \Delta t\cdot \color{red}{\theta_{k+1}} \end{array}\right. \\[2em] \stackrel{\text{Jacobian}}{\Longrightarrow} \quad \mathbb{J}_{EC} = \begin{pmatrix} 1 & \Delta t \\ -\Delta t & 1 \color{red}{-\Delta t^2} \end{pmatrix} = \underbrace{\begin{pmatrix} 1 & 0 \\ -\Delta t & 1 \end{pmatrix}}\limits_\text{"kick": update $p$} \cdot \underbrace{\begin{pmatrix} 1 & \Delta t \\ 0 & 1 \end{pmatrix}}\limits_\text{"drift": update $\theta$} $$

$\implies$ Euler-Cromer method is sometimes referred to as drift-kick algorithm

Implement in Python

In [18]:
def solve_eulercromer(theta, p, dt=0.1):
    ### from Euler:
    theta_next = theta + dt * p / (m * L*L)
    p_next = p - dt * m * g * L * np.sin(theta_next)
    return (theta_next, p_next)
In [19]:
results_eulercromer = np.zeros((n_steps, 2), dtype=np.float32)
results_eulercromer[0] = (theta_ini, p_ini)

for k in range(1, n_steps):
    results_eulercromer[k] = solve_eulercromer(*results_eulercromer[k - 1])
In [20]:
plt.contour(TH, PP, HH, levels=10, linestyles='--', linewidths=1)

plt.plot(results_euler[:, 0], results_euler[:, 1], c='b', label='Euler')
plt.plot(results_eulercromer[:, 0], results_eulercromer[:, 1], c='c', label='Euler-Cromer')

plt.legend(bbox_to_anchor=(1.05, 1))
set_axes()

What about energy conservation now?

In [21]:
plt.plot(
    hamiltonian(results_euler[:, 0], results_euler[:, 1]), 
    c='b', label='Euler')
plt.plot(
    hamiltonian(results_eulercromer[:, 0], results_eulercromer[:, 1]), 
    c='c', label='Euler-Cromer')
plt.axhline(hamiltonian(theta_ini, p_ini), c='r', label='theory')

plt.xlabel('Steps $k$')
plt.ylabel(r'$\mathcal{H}(\theta, p)$')
plt.legend(bbox_to_anchor=(1.05, 1));

$\implies$ still finite error -- but bound within an interval around the correct solution!

(In fact, a modified Hamiltonian $\mathcal{K}$ is conserved...)

Adding Mid-point Rule: $\mathcal{O}(\Delta t^3)$

Störmer-Verlet (or "leapfrog") method: staggered update, formulate as drift-kick-drift!

leapfrog method sketch $$\left.\begin{array}\, \cfrac{d\theta}{dt} &= \cfrac{p}{mL^2} \\ \cfrac{dp}{dt} &= -m g L\sin\theta \end{array}\right\} \quad \stackrel{\text{leapfrog}}{\Longrightarrow} \quad \left\{\begin{array}\, \theta_{\color{red}{k+1/2}} &= \theta_k + \color{red}{\cfrac{\Delta t}{2}}\cdot\cfrac{p_{k}}{mL^2} \\ p_{k+1} &= p_k - \Delta t\cdot m g L\sin\theta_\color{red}{{k+1/2}} \\ \theta_{\color{red}{k+1}} &= \theta_{\color{red}{k+1/2}} + \color{red}{\cfrac{\Delta t}{2}}\cdot\cfrac{p_{\color{red}{k+1}}}{mL^2} \end{array}\right.$$
$\implies$ widely used symplectic algorithm: stable, second-order and time-reversible!

Exercise: verify that Jacobian of leapfrog algorithm gives $\det\left(\mathbb{J}_\text{leapfrog}\right) = 1$

In [22]:
def solve_leapfrog(theta, p, dt=0.1):
    theta_half = theta + dt / 2 * p / (m * L*L)
    p_next = p - dt * m * g * L * np.sin(theta_half)
    theta_next = theta_half + dt / 2 * p_next / (m * L*L)
    return (theta_next, p_next)
In [23]:
results_leapfrog = np.zeros((n_steps, 2), dtype=np.float32)
results_leapfrog[0] = (theta_ini, p_ini)

for k in range(1, n_steps):
    results_leapfrog[k] = solve_leapfrog(*results_leapfrog[k - 1])
In [24]:
plt.plot(
    hamiltonian(results_euler[:, 0], results_euler[:, 1]), 
    c='b', label='Euler, $\mathcal{O}(\Delta t^2)$')
plt.plot(
    hamiltonian(results_eulercromer[:, 0], results_eulercromer[:, 1]), 
    c='c', label='Euler-Cromer, $\mathcal{O}(\Delta t^2)$')
plt.plot(
    hamiltonian(results_leapfrog[:, 0], results_leapfrog[:, 1]), 
    c='k', label='leapfrog, $\mathcal{O}(\Delta t^3)$')
plt.axhline(hamiltonian(theta_ini, p_ini), c='r', lw=2, label='theory')

plt.ylim(0.5, 0.6)
plt.xlabel('Steps $k$')
plt.ylabel(r'$\mathcal{H}(\theta, p)$')
plt.legend(bbox_to_anchor=(1.05, 1));

Let this sink in...

Are symplectic algorithms always a good idea? (When not...?)

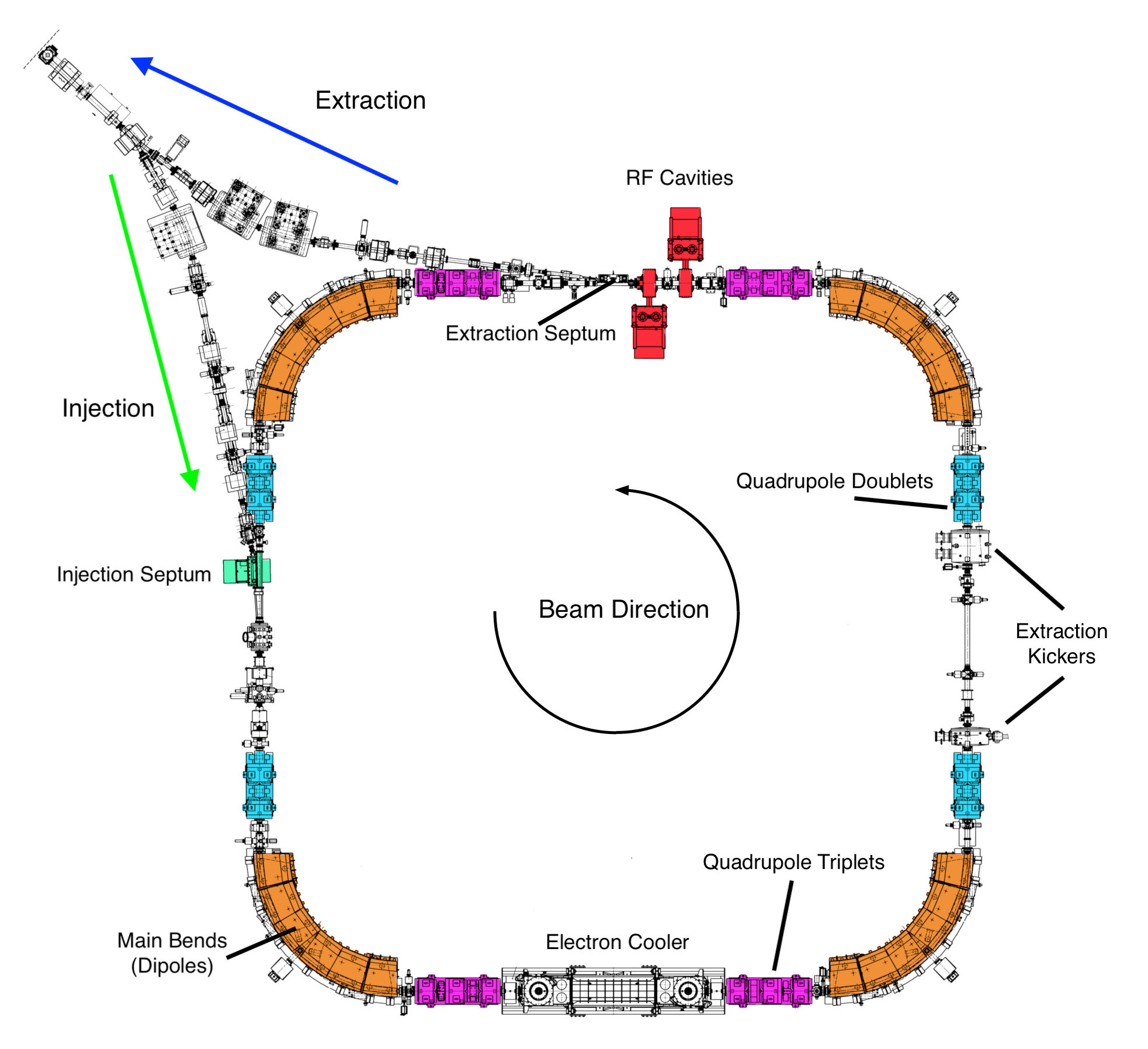
CERN LEIR layout

Analogy of Pendulum with Accelerator

Phase focusing with rf cavities:

  • particles drift over most of the circular accelerator
  • particles get kicked only in rf cavities
    (energy change through standing electromagnetic wave)

$\implies$ closely corresponds to discrete pendulum situation!

rf focused beam of particles $\leftrightarrow$ collection of pendulums

image: LEIR layout, CERN

Summary

  • time scales in accelerator physics
  • phase space & Hamiltonian functional
  • discrete numerical integration schemes:
    • Euler
    • Euler-Cromer
    • Leapfrog
  • symplecticity

Literature:

  • symplectic integrators: https://young.physics.ucsc.edu/115/leapfrog.pdf